- Matthew Mauntel
- Graduate Research Assistant
- Presenter’s NSFRESOURCECENTERS
- Florida State University
- Ashish Amresh
- http://dt.asu.edu
- Research Scientist
- Presenter’s NSFRESOURCECENTERS
- Arizona State University
- Zachary Bettersworth
- https://www.researchgate.net/profile/Zachary-Bettersworth
- Teaching/Research Assistant
- Presenter’s NSFRESOURCECENTERS
- Arizona State University
- David Plaxco
- http://www.davidplaxco.com
- Assistant Professor
- Presenter’s NSFRESOURCECENTERS
- Clayton State University
- Michelle Zandieh
- Professor
- Presenter’s NSFRESOURCECENTERS
- Arizona State University
Vector Unknown: A Game about Linear Combinations
NSF Awards: 1712524
2022 (see original presentation & discussion)
Grades 6-8, Grades 9-12, Undergraduate, Informal
Enter the 3D world of Pirate's Cove - a serious game designed developed to explore and visualize the concepts of taking linear combinations of vectors and matrix transformations. The game was developed as a collaboration between mathematics educators, game designers, and a capstone class at Arizona State University. As players explore the island they learn about taking linear combinations in one, two, and three-dimensions, explore matrix multiplication, and explore different bases for three-dimensional space while growing their horde of treasure on a pirate's ship. The project included development of the game, interviewing students for their reasoning about the game, and development of classroom materials to support the game.
Related Content for Vector Unknown: Pirates Cove a 3D Vector Exploration
-
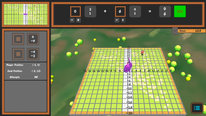 2021Vector Unknown: A Game about Linear Combinations
2021Vector Unknown: A Game about Linear Combinations
Matthew Mauntel
-
 2020Vector Unknown: A Game About Vectors and Linear Combinations
2020Vector Unknown: A Game About Vectors and Linear Combinations
Matthew Mauntel
-
 2020Pirate Math Equation Quest
2020Pirate Math Equation Quest
Sarah Powell
-
 2022SEERNet: Catalyzing innovative research on digital learning
2022SEERNet: Catalyzing innovative research on digital learning
Stefani Pautz Stephenson
-
 2022Empathy at the Heart of Design
2022Empathy at the Heart of Design
Lara Hebert
-
 2022World Building On Mars: Letting Student Idea Shine
2022World Building On Mars: Letting Student Idea Shine
Shannon Schmoll
-
 2022Get the Facts Out: Repairing the Reputation of STEM Teaching
2022Get the Facts Out: Repairing the Reputation of STEM Teaching
Wendy Adams
-
 2017Graspable Math: A Dynamic Algebra Notation for Math Learning
2017Graspable Math: A Dynamic Algebra Notation for Math Learning
David Landy





Mark DeLoura
Love that you're using games for education... have you been able measure efficacy?
Have you considered finding ways to have students create their own games as a way of increasing their depth of knowledge on a subject?
Matthew Mauntel
Graduate Research Assistant
Hello Mark, thank you for the question. We've collected qualitative data about students strategies for completing the game and examined some data from homework assignments relating to the game as well. We are currently working on designing a pre/post-test and will be comparing it with student scores in the game, but have not completed this research yet.
In terms of creating their own games. I can approach this from two different angles. The first angle is that we had computer science students design both games (2D and 3D) for a capstone project. This required the students to think deeply about the mathematics being presented in the game and how best to represent it in the game. It also required some linear algebra developing tilts, rotations, grid development, and placement of goals. I would say the project was an overall success in not only designing the games, but also having these students be exposed to the mathematics behind the game.
Second, for my dissertation, I am had students play the 2D game, analyze the game, and create a mock 3D game that they could play in GeoGebra. These students had not taken linear algebra before and had a mixture of experience with gaming. Some of them had not even plotted points in 3D before. I found the intersection between thinking about the game and designing a game to be overall very fruitful. For example, the students had to create easy, medium, and hard levels and this allowed the students structure their thinking and communicate which concepts they found most difficult. Concepts borrowed from the original playthrough, such as the limitation of the coordinate axis to +/-20 allowed the students to explore linear combinations that would work in a limited 2D environment. While exploring this limited environment, they discovered aspects such as linear independence and dependence. Also, I had one group that tried to make a "bluff" vector as a prospective answer. This gave rise to the question of what vectors would not work for a problem. For example, one student proposed switching the goal coordinates as a "bluff." Then there was an interesting discussion about if this was actually a bluff vector.
All in all, I found having students design their own game to be very fruitful. The linear algebra students were not experts in game design, but from the playing the game they could obtain structures that they could try to mimic and could be used to organize their thoughts for productive mathematical discovery. This is my first pass at this type of research, and I think more time would have to utilized for developing such materials towards targeted goals for a course (but it could be very productive as a class project).
Nathan Holbert
Associate Professor
Thanks for sharing this interesting project! I'm curious about your design process with the ASU students. We know good learning games integrate the target concepts with game mechanics (rather than have learning and game be separate), but this is hard to do well! The video shows some clever interactions for each level such as manipulating the scalar quantities to dictate the location of the grappling hook. Can you say a bit about the ways in which your team has thought about integrating mechanics and target concepts, and also how that came about? Were these mechanics proposed by the ASU team? Or what kind of conversations or activities did you enact as a team to collaboratively build gameplay that thoughtfully integrates the target concepts?
Matthew Mauntel
Graduate Research Assistant
Nathan, thank you for your question. I would say this was a collaborative effort. The team consisted of an expert game designer, two math ed researchers, and a few graduate students in addition to the ASU capstone students. The math ed researchers met and discussed what topics they wanted to develop in the game. I will say that one was an expert in mathematical metaphors which students use while taking linear algebra. The capstone students met with the math ed researcher and the game design expert who was teaching the class in order to discuss the material covered in the game and several ways the researchers envisioned the game (in particular there is a travel metaphor that is popular for students to use while discussing linear combinations and both researchers wanted this metaphor incorporated into the game in some way). I would say the overall process was very collaborative.
Students were given material from the Inquiry Oriented Linear Algebra curriculum (https://iola.math.vt.edu/) to help form the basis for their understanding in addition to the discussions in the meetings. They would often present their example programs and there was a back and forth that balanced gameplay with incorporation of the concepts. For example, one aspect of the 2D game that was student proposed involved presenting students with four vectors with two pairs of linear dependent vectors which helped the player get a feel for the linear dependence. Another game that we are refining is a cannonball game that is fun (you blow up ships), but the gameplay initially was just calculating a lot of matrix multiplication. Through a discussion and experience with a task from the IOLA curriculum we are changing the mechanics to better resemble a task that explores change of basis.
In summary, I would say that the design process was balanced by having students need to design an interesting game and the mathematics educators having knowledge from both teaching and researching the topics providing insight guiding this process. In particular thinking about contexts inspired by mathematical metaphor research and and in-game decisions that mimic student thinking from researched curricular tasks.
Joshua Danish
Professor and Program Chair
Lots of interesting ideas here, thanks or sharing! You mentioned wanting to help the learners see "real" mathematical concepts / practices that they might engage in as graduate students. I wonder if you have a sense of whether students see the game-based-math as having real-world applications? Did your design incorporate any explicit scaffolds to help the students translate out to the real world? Thanks for sharing!
Matthew Mauntel
Graduate Research Assistant
Joshua, thank you for the question. I would say that when we use the word real, we do not necessarily mean real-world. Instead, we mean something that is experientially real for the students. I would say that a video game is an experientially real scenario that they can draw upon. I will say though that our team has worked to design materials for the classroom that connect to the game to bridge the students' gaming experiences to formal mathematics. In the class, they will do real-world problems, including a traffic flow problem that could use some concepts developed in the game.
On a side note, for my dissertation I had students design a 3D version of the game (this was before the 3D version of the game above was completed). Looking at the data, I found that students would use certain views in GeoGebra to do certain activities in 3D space. So for example, they would occupy one viewpoint to see if two vectors were linearly dependent. They would also create 2D projections to see if the projection of the vector (from their view) spanned that 2D space and then altered the view to see the tilt of a plane spanned by 2 vectors. These activities provide a context for students breaking down and orienting themselves to 3D space. They also provide important experiences that students can mimic when they are for example designing objects in CAD or doing some engineering projects. All in all I see the games as providing another resources that students can draw upon to solve problems and the more resources we provide to and connect mathematical ideas to the better.
Josh Sheldon
Project Lead
Nice work - as mentioned above, what I could see from the video of the game shows that it does integrate the mathematical concepts and practices into the game mechanics nicely. No Math Blaster here.
Many of my questions have already been covered, but I am curious to hear a bit more about any efficacy studies you've done (if you have). In particular, I wonder if you've tried using the game with players who would not typically be taking a linear algebra course. In other contexts, I've seen players who would not otherwise be considered "ready" for a particular piece of material have no problem picking it up through a game.
Finally, do you offer any additional scaffolding or opportunity to help players/learners formalize what they've uncovered, that is put the names of the techniques and objects with what they've experienced in the game?
Further posting is closed as the event has ended.