- Andrew Izsak
- Professor
- Presenter’s NSFRESOURCECENTERS
- University of Georgia
- Sybilla Beckmann
- https://faculty.franklin.uga.edu/sybilla/
- Meigs Distinguished Teaching Professor
- Presenter’s NSFRESOURCECENTERS
- University of Georgia
- laine bradshaw
- https://coe.uga.edu/directory/profiles/laineb
- Associate Professor
- Presenter’s NSFRESOURCECENTERS
- University of Georgia
- Torrey Kulow
- Post Doctoral Researcher
- Presenter’s NSFRESOURCECENTERS
- University of Georgia
Investigating Proportional Relationships from Two Perspectives
NSF Awards: 1420307
2016 (see original presentation & discussion)
Grades 6-8
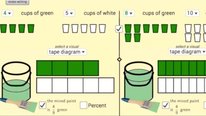
The Investigating Proportional Relationships from Two Perspectives project is investigating how future mathematics teachers in preparation programs at the University of Georgia develop facility reasoning about proportional relationships in terms of quantities. We are attempting to make three significant contributions to teaching and research about proportional relationships—arguably the most central mathematics in the middle grades. First, we are investigating a new, potentially transformative approach to proportional relationships that is based on two complementary perspectives, one that makes co-variation visually explicit with double number lines and one that makes multiplicative relationships between quantities visually explicit with strip diagrams. The central hypothesis for InPReP2 is that, taken together, the two perspectives may facilitate both key features of proportional relationships and open new pathways that make subsequent topics, like linear equations and statistical samples, more accessible. Second, we are investigating new, potentially transformative methods that coordinate detailed case studies with recent advances surveying multiplicative reasoning in large, national samples. Third, we are examining how different initial strengths and weaknesses with multiplicative reasoning affect how future teachers make sense of the two perspectives on proportions and applications. By examining a potentially transformative approach to ratio and proportional relationships, the project will generate results about multiplicative reasoning that can inform improved teacher education content courses and professional development that prepare teachers cross the nation for standards that emphasize sense making with quantities, including the Common Core State Standards. Thus, the project has high potential for improving teaching and learning middle grades mathematics fundamental to subsequent college readiness.
Related Content for Proportional Relationships from Two Perspectives
-
2017Investigating Proportional Relationships
Andrew Izsak
-
2016CAREER: Algebraic Knowledge for Teaching
Meixia Ding
-
2015Math Snacks
Barbara Chamberlin
-
2015Re-imagining Video-Based Online Learning
Joanne Lobato
-
2016An Exploration of Best Mentoring Practices of STEM Program
Germysha Little
-
2018Crosscutting Concepts: Progressions in Earth Systems
Jon Boxerman
-
2016Visual Access to Mathematics: Supporting Teachers of ELs
Johannah Nikula
-
2019Differentiating Mathematics Instruction for Middle School
Amy Hackenberg
E Paul Goldenberg
Distinguished Scholar
Watching a brief video and taking a full course are naturally quite different but I noticed that I had to watch two video segments—the transfer of the gold grams per part to the copper parts (1:55 in your video), and the expanding/contracting parts (2:25)—twice to see what you were doing. What (if any) places in your work do you find teachers needing to “look twice”? Do you see any cases (especially in the first representation) in which teachers seem to get the “method” but not understand the idea? This is, by the way, very intriguing work!
Andrew Izsak
Professor
Hi Paul,
Thank you for the question. In our experience working with preservice teachers and talking to mathematics education colleagues, thinking about proportional relationships from the variable parts perspective takes time to develop. We devote several weeks to developing the perspective in courses for future middle and secondary grades teachers. We pose tasks and allow students to reason with strip diagrams and develop methods that make sense to them. We have found that working on proportional relationships helps teachers deepen their understandings of measurement and partitive division.
Andrew, Sybilla, and Torrey
E Paul Goldenberg
Distinguished Scholar
Thanks, all. I assume it’s too early to know how this shows up in these preservice teachers’ (future) teaching, but will that at some point be part of this study? I always wish we had more time for longitudinal views!
Miriam Gates
Researcher
I was very interested in this work. I am curious, though, about the use of variable parts. You note in the video that this is the first such application in the US. I’m curious if this method has been used elsewhere and what lessons, if any, you have drawn on in implementing this approach with your teachers.
Andrew Izsak
Professor
Hi Miriam,
Our inspiration comes from Japanese and Singapore curricula. That said, we have developed all of our own activities for use in teacher education courses. We continue to experiment with tasks that help future teachers reason with variable parts. Thank you for your interest in our work.
Andrew, Sybilla, an Torrey
Miriam Gates
Researcher
Thanks for your response. Are some sample tasks available somewhere?
Sybilla Beckmann
Meigs Distinguished Teaching Professor
Hi! If you look through some of the slides from our presentations on our website:
http://temrrg.wix.com/temrrg
you will find some of the tasks we have used there.
Courtney Arthur
What does your teacher professional development entail? How long and what is the focus (primarily engaging in mathematics, focusing on pedagogy, etc?)
Andrew Izsak
Professor
Hi Courtney,
The project is situated in mathematics content courses for teachers. In the middle grades preparation program multiplication, division, and fractions are developed in a fall semester-long course on number and operation. The two perspectives on proportional relationships are developed in the subsequent spring course on algebra. In the secondary grades preparation program, these topics are the backbone of a semester long content course on multiplication. I think we are fairly unusual in requiring a semester long course on multiplication topics for future secondary teachers, but in our experience it is much needed. Pedagogy is covered in separate courses.
Andrew
Chad Paul
I was a little confused by the video. The posed question said the ratio of gold : copper is 7:5 and ask how much gold needed to be mixed with 25 grams of copper but the variable parts diagram seems to reverse this. On the other hand, the direct variation seemed to fit the original ratio, so I thought I would ask.
That said, I like the way you tie everything back to the meaning of multiplication.
Sybilla Beckmann
Meigs Distinguished Teaching Professor
Good catch! There was an error in the statement of the problem. I’m sorry we missed that. In the statement, it should have said that there was 25 grams of gold. The solution that is presented goes along with that.
Further posting is closed as the event has ended.