The Impact of a Teacher-Led Early Algebra Intervention on Children's Algebra...
R305A140092
2018 (see original presentation & discussion)
Grades K-6
This video will showcase evidence that children in elementary grades can engage in algebraic thinking in powerful ways. We will briefly discuss the framework for early algebra that guides our work and how this has informed the design of a curricular intervention for developing children's algebraic thinking. We will share findings from a randomized study of the efficacy of our intervention, across Grades 3 – 5, when it is implemented by teachers as part of their regular classroom instruction. In particular, we will share results on how children in Grades 3-5 develop longitudinally in their algebraic thinking, including growth in their use of algebraic strategies to solve non-routine problems.
Related Content for Impact of a Teacher-Led Early Algebra Intervention
-
 2015Algebraic Knowledge for Teaching
2015Algebraic Knowledge for Teaching
Meixia Ding
-
 2017Young Children's (K-1) Understanding of Algebraic Thinking
2017Young Children's (K-1) Understanding of Algebraic Thinking
Bárbara Brizuela
-
 2017Preparing Student for Success in Algebra
2017Preparing Student for Success in Algebra
Maria Blanton
-
 2022Math for All: Understanding How Diverse Students Learn
2022Math for All: Understanding How Diverse Students Learn
Babette Moeller
-
 2018MathByExample: Dislodging Misconceptions in Grades 4/5
2018MathByExample: Dislodging Misconceptions in Grades 4/5
Allie Huyghe
-
 2016CAREER: Algebraic Knowledge for Teaching
2016CAREER: Algebraic Knowledge for Teaching
Meixia Ding
-
 2022Math+C: Mathematics through Programming in Grades 2–5
2022Math+C: Mathematics through Programming in Grades 2–5
Deborah Spencer
-
 2022Teaching Early Algebra through Example-Based Problem Solving
2022Teaching Early Algebra through Example-Based Problem Solving
Meixia Ding

Maria Blanton
Senior Scientist
Welcome! This video provides an overview of findings from the first three years of a large-scale longitudinal study. As described in the video summary, we implemented an early algebra instructional sequence in grades 3-5 and tested the impact of this intervention on students' growth in algebra understanding as compared to a business-as-usual control condition. The students who participated in this study are now finishing up grade 6 and are again being assessed so that we can continue to examine and compare growth in algebra understanding one year post-intervention.
Do you have experiences as a teacher or researcher engaging elementary students in algebraic thinking? Where in the elementary math curriculum do you see opportunities to engage students in such thinking? What success stories or challenges would you like to share?
Do you have experiences as a teacher or researcher engaging secondary students in algebraic thinking? Where do you see successes and where do you see challenges? Are there particular algebraic concepts with which you see students struggle that perhaps could be introduced in the context of early algebra?
Thanks so much for watching our video and contributing to the discussion!
Courtney Arthur
This is a very interesting project! As a former 8th grade Algebra teacher I am all too familiar with students who would struggle with basic algebraic concepts. I am curious whether you find the barrier to be more with the language and understanding of vocabulary or with the application and ability to reason within/higher order thinking? At a younger age, I imagine it could be a combination of both?
Maria Blanton
Senior Scientist
Hi, Courtney. Good question. In the early grades, students do learn some vocabulary (e.g., "conjecture," "variable," and [function] "rule"), but this vocabulary is introduced gradually and in context and repeated and practiced often. We don't expect elementary students to talk about "polynomials" or use overly complex language. The same can be said for the concepts. We focus on a few big ideas as outlined in the video and really spend time developing them. We are interested in laying the foundation so that by the time these students reach 8th grade algebra the more formal mathematics makes sense. Thank you for watching!
Dave Barnes
Associate Executive Director
Hi Maria! As you look at developing students' growth in the Big Algebra Ideas - Expressions, Equations, Equality & Inequality, Functional Thinking, and Generalized Arithmetic - how do you think about the sequencing and connecting these ideas through the development? Is it more of a building from one to the other or spiraling through the big ideas?
Similarly do you see Thinking Practices as being evident through the development of each Big Algebra Idea?
Lastly what do the students think about learning algebra and mathematics in this way?
Maria Blanton
Senior Scientist
Hi Dave, thank you for your question.
(This is Despina Stylianou, by the way, responding on behalf of the LEAP team). In this work, we designed a sequence of lessons across grades 3-5. Each grade level sequence consisted of 18 one-hour lessons which were designed to build in complexity over time and to engage students in a range of critical algebraic thinking practices (generalizing, representing, justifying, and reasoning with mathematical structure and relationships) as they occur in the context of different big ideas (as you mentioned, too, generalized arithmetic; equivalence, expressions, equations, and inequalities; and functional thinking).
While different lessons addressed mainly one big idea, overall, we spiraled through the big ideas and revisited them in different lessons as well as in the three years of this work. For different children different ideas appeared to develop at different times, and growth was reported on all ideas throughout the duration of the project.
The "thinking practices" as you mentioned above, that we called core algebraic practices characterized all lessons and were a critical component of the instruction. In fact, one significant finding of this study was that students whose teachers engaged more deeply and more frequently in these core algebraic practices in their instruction performed higher than students whose teachers engaged less in these practices.
We did not examine students dispositions towards learning or early algebra. Perhaps that's something to consider in the future. Thanks for watching!
Louis Gross
Director and Professor
Maria et al., Thanks for an enticing summary of this project and for ll you have been doing to advance student mathematical understanding. As this is a quite large study, I expect that you will have the statistical power available to detect the kinds of pre- and post-intervention effects you described briefly. What other outcomes and impacts do you have planned to investigate and how fine-resolution will the data be in terms of picking apart individual student factors and the effects of the intervention?
Maria Blanton
Senior Scientist
Hi Louis, thank you for taking the time watch our video! This is Rena Stroud, the LEAP team’s quantitative methodologist.
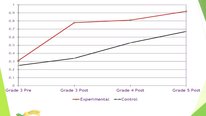
Our primary focus is whether or not students who received the LEAP intervention in grades 3 through 5 outperformed students who received their school’s traditional curriculum. We are in the midst of our longitudinal analysis at the moment, in which we are employing a 3-level longitudinal piecewise hierarchical linear model. We chose the piecewise model since our descriptive data suggests that there is a significant bump in performance in the first year of the study (grade 3 pre-test to grade 3 post-test), followed by a possible leveling off of that effect across grades 4 and 5. However, it appears that students in the treatment condition maintain their advantage over the entirety of the intervention. As you mentioned, given the size of our sample (over 3000 students from 46 schools), we do have the statistical power to detect an effect here.
Given that our randomization occurred at the school level, we are primarily interested in school-level factors. In our multilevel analyses, we are taking into account school-level SES (the percent of students in each school receiving free or reduced-price lunch), treatment condition, as well as the interaction between those two variables, which would allow us to explore whether the treatment is equitable across the range of SES. We have relatively little student-level data other than student gender, and recognize that this is an area to consider in future research.
In terms of outcomes, in addition to correctness, we are also interested in the types of strategies that students use, particularly those that are algebraic in nature. Specifically, we are interested in students’ use of structural strategies, those that go beyond a focus on the surface features of an item. We are exploring separate multilevel models to examine the impacts of the intervention on both outcome measures. Individual item analyses are also undertaken when warranted.
Finally, we are invested in exploring the fidelity with which teachers implement the intervention. To that end, we asked all teachers to complete logs regarding their practice, and we also interviewed a subset of teachers and observed (videotaped) a sample of classrooms. We are currently exploring the relationship between teachers’ fidelity of implementation (FOI) and student performance as another area of impact. Thank you for your thoughtful comments!
Louis Gross
Director and Professor
Rena, thanks for the detailed response. It is good to know that the evidence indicates there is no loss of advantage over time. Does this also hold for students in the treatment in grade 3 and then on non-treatment in later grades? Or is that not possible to assess due to the design?
Maria Blanton
Senior Scientist
Students in the treatment condition receive the LEAP intervention for all three years, and those in the control condition receive regular instruction for the same time period. Our preliminary analyses seem to indicate that the intervention is most effective in the first year - this is where kids in the treatment condition get the biggest bump in performance compared to controls. Participation in the following two years seems to help maintain the advantage (control kids are not "catching up" so to speak), but the increase in performance is not as steep (relative to controls) as it was in year 1. I hope this helps to clarify!
Nicole Kee
Hi Maria,
I currently teach 8th grade Algebra, Pre-Algebra, and Geometry and most certainly see the importance of introducing algebraic thinking at an early age. The results that you have found so far are great and I look forward to seeing what happens with the results as the levels of math continue to increase. The students that I teach that generally struggle with math often have trouble with comprehending word problems in our pre-algebra course. For instance when we teach rate of change our students often struggle with applying the algebra content to the real world and struggle with seeing slope through multiple representations, whether it be a graph, table, or equation. Do you predict that the group of students that have been introduced to this program will be able to take an application problem in an algebra course and can accurately make connections across multiple representations? Additionally, are you looking at the impacts of this program with students that may have learning disabilities?
I am interested in finding out more about the PD development that you put in place in order to help build these algebra foundations.
Thanks!
Maria Blanton
Senior Scientist
Hi Nicole,
Thanks for your question. My name is Angela Murphy Gardiner and I am a teacher and researcher on Project LEAP. In grades 3-5 we do multiple problems in the functional thinking domain. Within these lessons students are introduced to real world problems and represent the data in multiple ways (function table and graphing). Students are doing really well in this area. They are able to graph and make interpretations based on their graphs and tables. This of course is the early stages, but we believe this is setting them up to be very successful when they get to you and discussions about slope really begin to take shape.
As for the PD, we met with teachers for a day in the summer to introduce them to early algebra big ideas and key practices. We then met with them for a half day monthly (September-April). During these sessions we walked them through each of the lessons they would be teaching and provided them opportunities to solve the problems on their own, ask questions about the problems and we showed them classroom videos so they could see how elementary students think through the problems. I was also available to teachers via phone or email if they had any questions between our meetings. We did our best to provide as much support as possible for our teachers.
We have a new project that we are in the early stages of, working with students in K-2. This project focuses on students in culturally diverse districts and students with learning disabilities. We will have data on this in the coming years, and it is a project we are very excited about.
Thanks again for your questions.
Further posting is closed as the event has ended.